Geometry Theorem from Antiquity
27 May
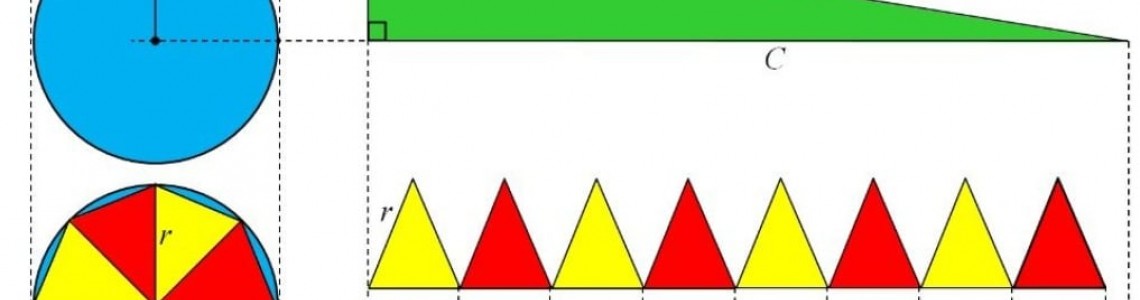

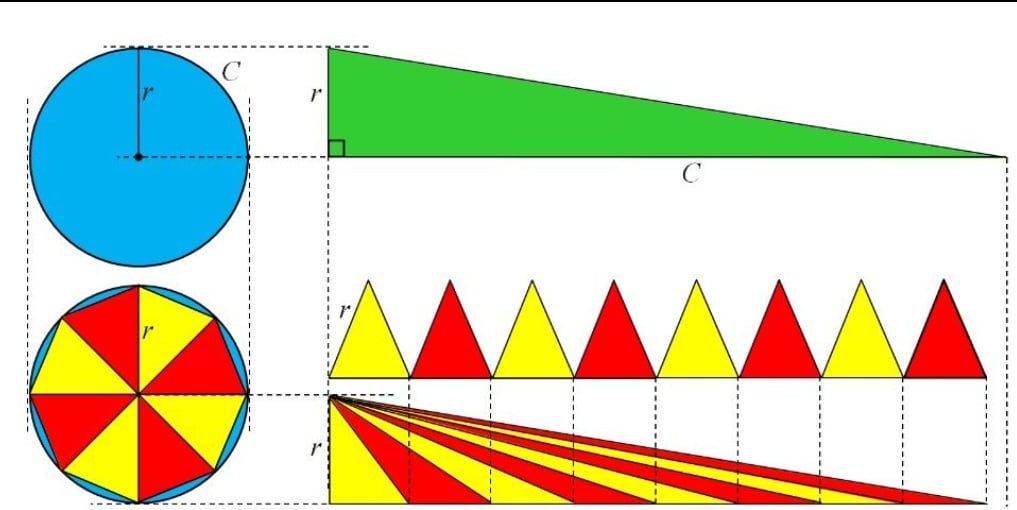
Here is an amusing little Geometry Theorem from Antiquity:
"The area of a circle of radius r and circumference C is identical to that of a right triangle of height rand base C."
This is very simple to prove and can be used as basic prototype to derive the area of a circle.
Archimedes (3rd century BCE) established his circle area equality in an essay ‘Measurement of a circle’ in which he also famously used infinite sequences of inscribed and circumscribed polygons to approximate the ratio of circumference to diameter. Euclid’s proof of his Proposition 2,Book XII (c.300BCE) is a similar application of the method of exhaustion but Archimedes attributes the method to Eudoxus a century earlier.